Wilhelmy plate method
Method for measuring the surface tension (SFT) of a liquid, the interfacial tension (IFT) between two liquids and the contact angle between a liquid and a solid. The force acting on a vertically immersed plate is measured.
Background
When a vertically suspended plate touches a liquid surface or interface, then a force F, which correlates with the surface tension or interfacial tension σ and with the contact angle θ according to the following equation, acts on this plate:

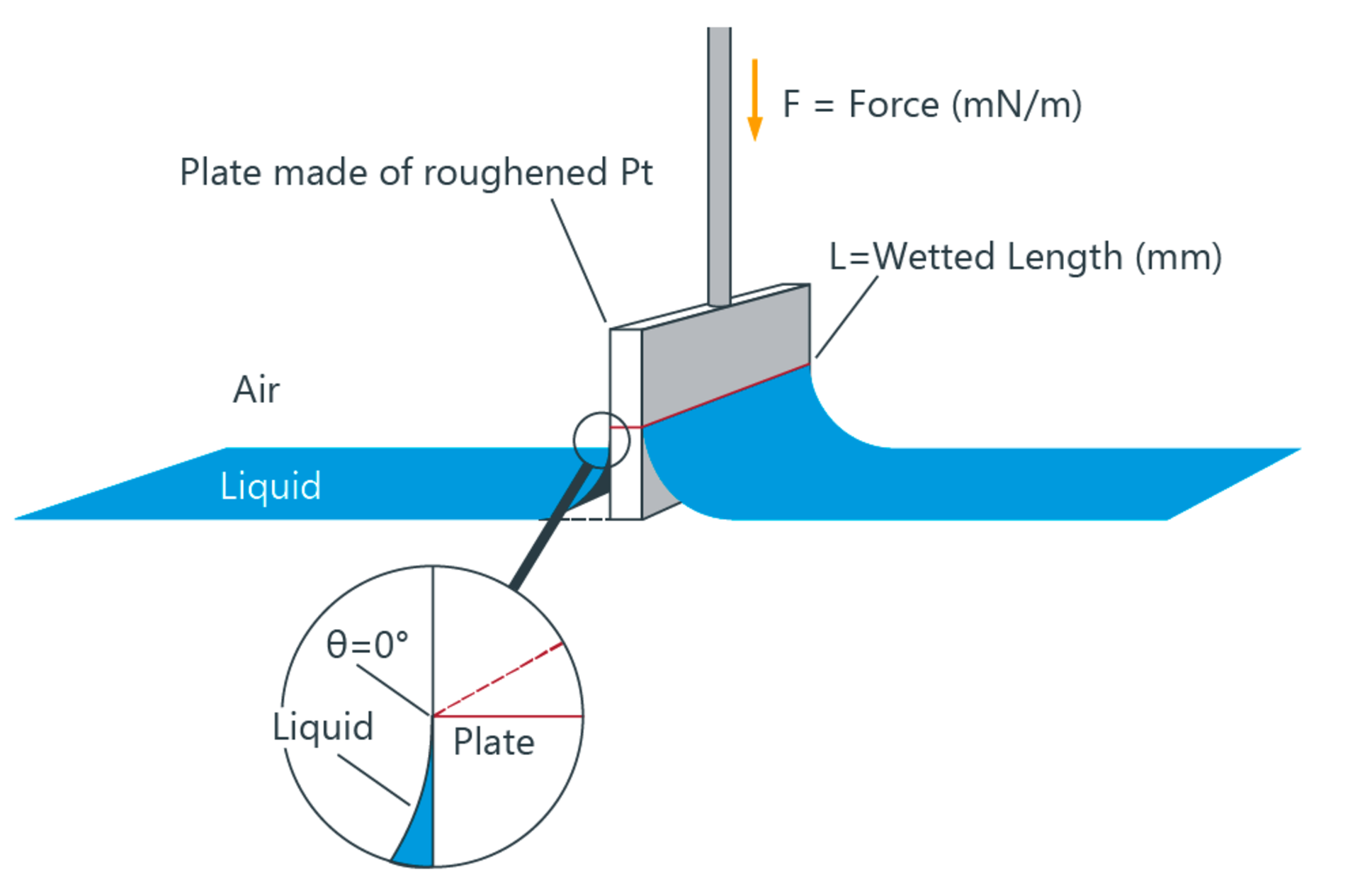
The wetted length L of the plate is equal to its perimeter. To measure the force F, the plate is attached to a force sensor of a tensiometer.
Measuring methods
- Measurement of the surface tension or interfacial tension: Platinum is chosen as the plate material when measuring the SFT or IFT as it is chemically inert and easy to clean, and because it can be optimally wetted on account of its very high surface free energy and therefore generally forms a contact angle θ of 0° (cos θ = 1) with liquids. The required variable σ can be calculated directly from the measured force. Unlike the quasi-static ring method according to du Noüy, in which the surface is deformed during the measurement, the plate method is purely static. This makes it possible to record the change in SFT or IFT with respect to time as well as the end values at equilibrium.
- Measurement of the contact angle: To measure the contact angle, the solid sample - which is usually in plate form - is immersed in a liquid with known SFT. The contact angle can be calculated from the measured force by transposing the Wilhelmy equation:

With the Wilhelmy method, a dynamic contact angle is normally measured by slowly immersing and then withdrawing the solid. The advancing angle is determined during the wetting process and the receding angle during the de-wetting process.
The wetted length L of the solid (perimeter at the level of the liquid surface) must be known and must not be dependent on the immersion depth. In order to determine the wetted length, a measurement can be carried out with an optimally wetting (spreading) liquid with known SFT with which the contact angle is 0° (cos θ = 1).
Results for the Wilhelmy contact angle can be used to determine the surface free energy of the solid.

