Freie Oberflächenenergie (engl. surface free energy, SFE)
Als freie Oberflächenenergie (surface free energy, SFE) wird die Arbeit bezeichnet, die aufgewendet werden müsste, um die Oberfläche einer festen Phase zu vergrößern. Die SFE bestimmt maßgeblich die Benetzbarkeit von Festkörpern durch Flüssigkeiten. Sie ist daher eine wichtige Größe für die Optimierung von Beschichtungsvorgängen, aber auch jeder anderen Art von Fest-flüssig-Kontakt.
Wann spricht man von der SFE, wann von der Oberflächenspannung?
Die Begriffe SFE und Oberflächenspannung (OFS) sind physikalisch äquivalent. Im Sprachgebrauch wird in der Regel SFE für Festkörperoberflächen und OFS für Flüssigkeitsoberflächen verwendet. Gelegentlich wird aber auch von der OFS eines Festkörpers gesprochen.
Die SFE hat als Energie pro Fläche die Einheit mJ/m2 (Millijoule pro Quadratmeter), wobei häufig auch die äquivalente, für die OFS gängige Einheit mN/m (Millinewton pro Meter) verwendet wird. Das Formelzeichen lautet σ (kleines Sigma), seltener γ (kleines Gamma).
Das Wort Zusatz „frei“ sagt aus, dass es sich um den in mechanische Arbeit umwandelbaren Anteil der Energie handelt, in Abgrenzung von der inneren Energie, welche zusätzlich die wärmebezogene Entropie beinhaltet. In der Praxis wird der Zusatz „frei“ häufig weggelassen.
Was ist die Verbindung zwischen SFE und Benetzbarkeit?
Jedes System strebt einen Zustand möglichst geringer freier Energie an. Flüssigkeiten nehmen deshalb aufgrund der OFS bei gegebenem Volumen die kleinstmögliche Oberfläche ein; in der Schwerelosigkeit bilden sie kugelförmige Tropfen. Festkörper können ihre Oberfläche jedoch nicht durch Verformung minimieren. Sie können aber zur Reduktion der freien Energie eine Grenzfläche mit einer Flüssigkeit ausbilden, d. h. sie können benetzt werden. Deshalb hängt die SFE eines Festkörpers eng mit dessen Benetzbarkeit zusammen.
Wie lässt sich die SFE beeinflussen?
Gute Benetzbarkeit und eine entsprechend hohe SFE sind beispielsweise beim Verkleben und Beschichten oder auch beim Drucken erforderlich. In anderen Bereichen, etwa beim Korrosions- und Nässeschutz, muss die Benetzbarkeit reduziert werden. Eine Vielzahl von technischen Verfahren bereitet feste Oberflächen auf den Kontakt mit Flüssigkeiten gezielt vor – die meisten davon verändern direkt oder indirekt die SFE.
Die Erhöhung der SFE ist bei Kunststoffoberflächen von zentraler Bedeutung. Die bekanntesten Methoden sind Plasma-, Flamm- und Koronabehandlung, hinzu kommen chemische Verfahren mit Oxidationsmitteln. Die industrielle Reinigung entfernt niedrigenergetische Kontaminationen durch Fette oder Öle. Die Oberfläche zeigt im Anschluss eine höhere SFE.
Eine niedrige SFE und entsprechend geringe Benetzung wird in der Regel durch Beschichtung mit niedrigenergetischen Stoffen erreicht. Beispiele sind PTFE-beschichtete Kochutensilien oder der Einsatz von Ölen für den Korrosionsschutz.
Wie hängen die SFE und der Kontaktwinkel zusammen?
Das Maß für die Benetzbarkeit ist der Kontaktwinkel (KW) θ (kleines Theta), der meist optisch als Winkel am Schnittpunkt der Kontur eines Tropfens mit der Ebene der Oberfläche (= Basislinie) bestimmt wird. Gemäß der Young’schen Gleichung resultiert der KW aus einem Kräftegleichgewicht dreier Spannungs- bzw. Energiekomponenten, die jede für sich bestrebt sind, die Ober- bzw. Grenzfläche zu minimieren:
- Die SFE des Festkörpers, σs (s für "solid")
- Die OFS der Flüssigkeit, σl (l für "liquid")
- Die Grenzflächenspannung (GFS) zwischen Festkörper und Flüssigkeit, σls
Die dazu von Young aufgestellte Gleichung lautet:

Die folgende Illustration zeigt den Kontaktwinkel, resultierend aus dem Kräftegleichgewicht bei der Festkörperbenetzung nach Young:

Wie wird die SFE aus Kontaktwinkeldaten berechnet?
Wird der KW mit einer Flüssigkeit bekannter OFS gemessen, dann bleiben zwei Größen der Young'schen Gleichung unbekannt: die gesuchte SFE und die GFS. Der Schlüssel zur Lösung liegt daher in der Beschreibung der GFS.
Gäbe es beim Zweiphasenkontakt keinerlei Wechselwirkungen zwischen der flüssigen und der festen Oberfläche, dann würden sie sich wie zwei separate Oberflächen verhalten. Die GFS wäre dann die Summe von SFE und OFS; der Kontaktwinkel betrüge in diesem theoretischen Fall 180° (cos θ =-1).
Treten Wechselwirkungen zwischen den Phasen auf, was in der Praxis immer der Fall ist, dann reduziert sich die GFS um den aus den Wechselwirkungen resultierenden Energiebeitrag:

Es gibt verschiedene Modelle für Berechnung der SFE, die sich vorwiegengd in der Interpretation und Berechnung der Grenzflächenwechselwirkungen unterscheiden. Am geläufigsten ist die Unterteilung zwischen polaren und dispersiven Wechselwirkungsanteilen, wobei jeweils die SFE und die OFS in einem polaren und einen dispersiven Anteil gesplittet werden. Vereinfachend wird davon ausgegangen, dass zwischen den Phasen jeweils nur gleichartige Wechselwirkungen stattfinden, sodass polare nur mit polaren und dispersive nur mit dispersiven Anteilen der angrenzenden Phasen miteinander in Beziehung gesetzt werden.
Um die SFE zu bestimmen, werden Kontaktwinkel mit mindestens zwei Flüssigkeiten gemessen, bei denen sowohl die OFS als auch deren polare und dispersive Wechselwirkungsanteile bekannt sind. Zur Berechnung der SFE wird jeweils die Young‘sche Gleichung mit Gleichungen zur Berechnung der Wechselwirkungen kombiniert.
Was sind polare und dispersive Anteile der SFE?
Als polar werden relativ starke Wechselwirkungen bezeichnet, die durch permanente und lokalisierbare Asymmetrie der Elektronendichte in Molekülen entstehen. Diese führt zu positiven und negativen Partialladungen und entsprechend zu elektrostatischer Anziehung.Bei Flüssigkeiten ist das bekannteste Beispiel das Wasser, dessen Polarität für die hohe OFS verantwortlich ist. Glas ist ein typisches Beispiel für eine stark polare Festkörperoberfläche.
Dispersive Wechselwirkungen sind in der Regel schwächer; sie entstehen durch statistische Fluktuationen der Elektronendichteverteilung in einem Molekül, die zu temporären Ladungsdifferenzen an verschiedenen Orten führt. In deren Folge kommt es zu elektrostatischer Anziehung zwischen Molekülen. Alkane und einige Kunststoffe wie zum Beispiel Polyethylen oder Polypropylen bilden ausschließlich dispersive Wechselwirkungen aus. Das ist auch der Grund für die schlechte Benetzbarkeit vieler Kunststoffe durch Wasser.
Die oben genannten Vorbehandlungsmethoden erhöhen im wesentlichen den polaren Anteil der SFE und machen so den Kunststoff dem Wasser ähnlicher. Gemäß dem Zweikomponentenmodell sind Benetzung und Adhäsion dann maximal, wenn beim Festkörper und bei der Flüssigkeit nicht nur die SFE und die OFS übereinstimmen, sondern auch die jeweiligen polaren und dispersiven Anteile.
Die folgende Illustration zeigt die Benetzung und Adhäsion abhängig von polaren und dispersiven Anteilen. Die großen Hände symbolisieren polare, die kleinen dispersive Wechselwirkungen. Im oberen Bild sind die Wechselwirkungen identisch, was zu maximaler Adhäsion und einem Kontaktwinkel von 0° führt. Darunter ist ein Beispiel mit nicht identischen Wechselwirkungskomponenten dargestellt.
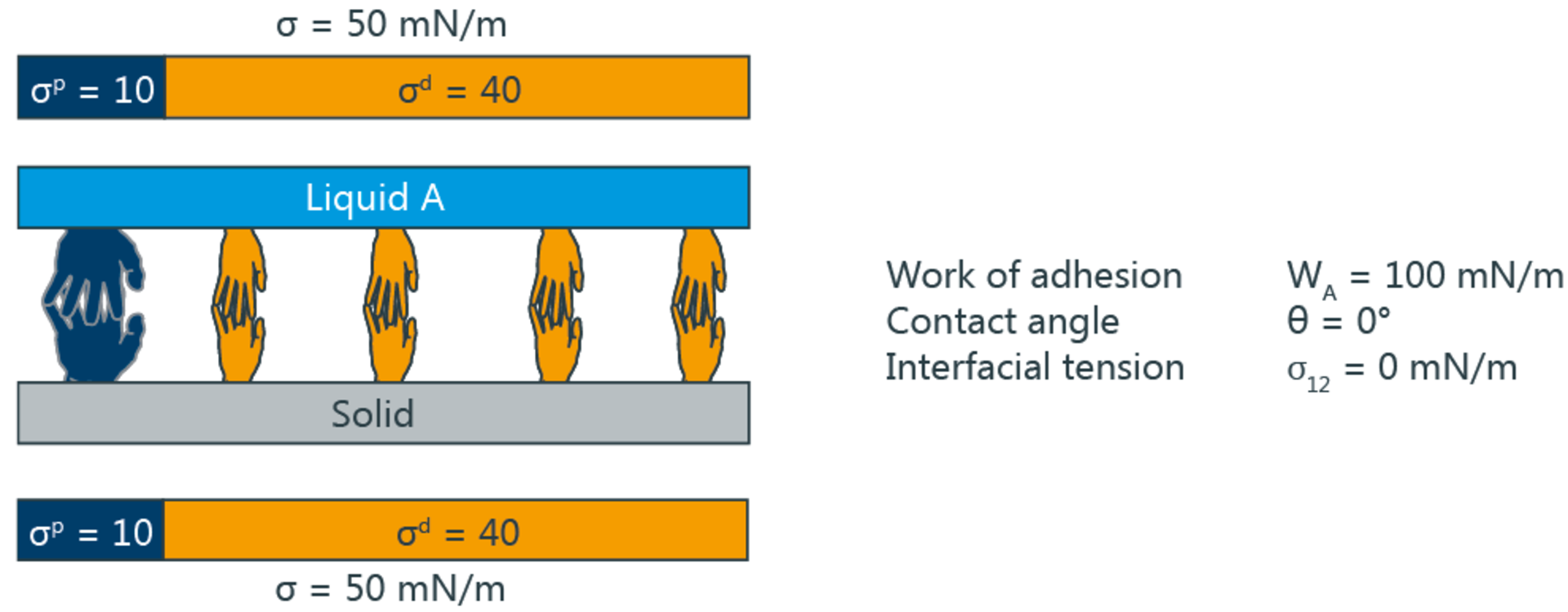

Welche Berechnungsmodelle für die SFE gibt es?
Von Fowkes stammt die erste wissenschaftliche Arbeit, in der die OFS von Flüssigkeiten in Wechselwirkungsanteile gesplittet und die SFE basierend auf diesen Anteilen mit Hilfe von Kontaktwinkelmessungen bestimmt wurde. Das heute am häufigsten verwendete Modell nach Owens, Wendt, Rabel und Kaelble (OWRK) geht auf Fowkes zurück und kommt mit Kontaktwinkeln zweier Flüssigkeiten mit bekannten polaren und dispersiven Anteilen der OFS aus. Weitere, seltener verwendete Modelle interpretieren die polaren und dispersiven Anteile anders als OWRK oder nehmen gar keine Interpretation der SFE und OFS bezogen auf deren Wechselwirkungsanteile vor. Die folgende Tabelle gibt eine Übersicht; Details zu den Modellen können in je eigenen Artikel dieses Glossars nachgelesen werden.
| Modell nach Autor(en) | Wechselwirkungungskomponenten der OFS |
|---|---|
| Fowkes | Dispersiver Anteil und nicht-dispersiver Anteil |
| Owens-Wendt-Rabel & Kaelble | Dispersiver und polarer Anteil |
| Wu | Dispersiver und polarer Anteil |
| Schultz | Dispersiver und polarer Anteil, Messung in umgebender flüssiger Phase |
| Oss, Good (acid-base) | Lewis-Säure-Anteil und Lewis-Base-Anteil |
| Extended Fowkes | Dispersiver und polarer Anteil und Anteil der Wasserstoffbrückenbindungen |
| Zisman | keine Zerlegung in Komponenten; Bestimmung der kritischen Oberflächenspannung |
| Neumann Equation of State | keine Zerlegung in Komponente |
Kann die SFE nicht auch mit Testtinten bestimmt werden?
Tintentests sind eine immer noch eingesetzte Methode, um die Benetzbarkeit von Oberflächen zu prüfen. Das Ergebnis wird von den Anwendern und auch von einigen Testtintenherstellern als SFE interpretiert. Die Methode ist scheinbar einleuchtend: Mehrere Flüssigkeitsgemische mit absteigender OFS werden nacheinander auf die Oberfläche aufgetragen. Die OFS der Flüssigkeit, die gerade einen nicht verlaufenden Film bildet, die Oberfläche also vollständig benetzt, wird mit der SFE des Festkörpers gleichgesetzt.
Die Beschaffenheit der Wechselwirkungen wird dabei jedoch außer Acht gelassen. Das hat zur Folge, dass die Ergebnisse des Tintentests sich auf den Kontakt mit den meisten anderen Flüssigkeiten nicht übertragen lassen. Im technischen Prozess verhält sich der Festkörper daher oft ganz anders, als nach dem Tintentest zu erwarten war.
Zur Veranschaulichung folgendes Beispiel: Das polare Wasser hat eine höhere OFS als das unpolare Diiodmethan (DIM), eine Standardflüssigkeit für die SFE-Bestimmung. Auf unpolaren Kunststoffen hat Wasser einen deutlich höheren Kontaktwinkel als DIM. Beim Kontakt derselben Flüssigkeiten mit sauberem Glas, einer sehr polaren Oberfläche, kehrt sich der Verhältnis um: Der Wasserkontaktwinkel ist zum Teil erheblich kleiner als der DIM-Kontaktwinkel. Das Beispiel zeigt, dass der Betrag der OFS allein nicht ausreicht, um eine Beziehung zwischen Benetzung und SFE herzustellen. Eine umfassende, kritische Auseinandersetzung mit der Testtintenmethode findet in der veröffentlichten wissenschaftlichen Studie Why Test Inks Cannot Tell the Whole Truth about Surface Free Energy of Solids statt (s. Literaturliste).
Literatur
- F. M. Fowkes, Attractive Forces at Interfaces. In: Industrial and Engineering Chemistry 56,12 (1964), P. 40-52.
- M. Jin, F. Thomsen, T. Skrivanek and T. Willers, Why Test Inks Cannot Tell the Whole Truth About Surface Free Energy of Solids. In: K. L. Mittal (Ed.), Advances in Contact Angle, Wettability and Adhesion Volume 2 , Hoboken, New Jersey and Salem, Massachusetts 2015, P. 419-438.
- D. H. Kaelble, Dispersion-Polar Surface Tension Properties of Organic Solids. In: J. Adhesion 2 (1970), P. 66-81.
- D. Owens; R. Wendt, Estimation of the Surface Free Energy of Polymers. In: J. Appl. Polym. Sci 13 (1969), P. 1741-1747.
- W. Rabel, Einige Aspekte der Benetzungstheorie und ihre Anwendung auf die Untersuchung und Veränderung der Oberflächeneigenschaften von Polymeren. In: Farbe und Lack 77,10 (1971), P. 997-1005.
- T. Young, An Essay on the Cohesion of Fluids. Philosophical Transactions of the Royal Society of London, The Royal Society, London 1805, Vol. 95, P. 65-87.






