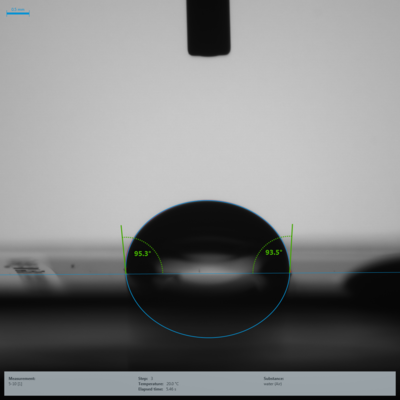
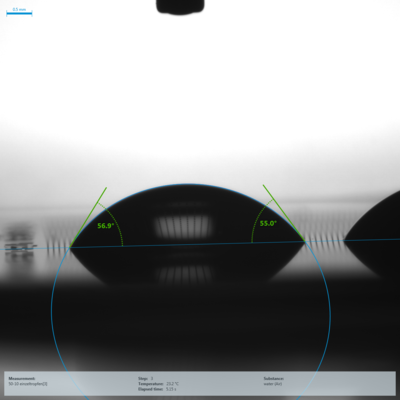
Benetzung und Rauheit – Was tun, wenn Wenzel nicht funktioniert?

Dass die Rauheit einer Oberfläche deren Benetzungsverhalten beeinflussen kann, ist bekannt und von Wenzel in seiner Theorie mit einer einfachen Gleichung beschrieben. Aber wie gut lässt sich diese Theorie auf die industrielle Praxis übertragen? Wir haben den Test gemacht und Siliziumwafer durch reaktives Ionenätzen sehr präzise mikrostrukturiert, ohne jedoch die chemische Struktur der Oberfläche und damit deren freie Oberflächenenergie zu verändern.

Mit Hilfe eines Konfokalmikroskops wurde die Mikrostruktur der Oberflächen nachgemessen, um die für Wenzels Theorie relevanten Parameter zu ermitteln. Kontaktwinkelmessungen auf den unterschiedlich strukturierten Proben wiesen überraschenderweise eine Wenzels Vorhersage entgegengesetzte Korrelation auf. Dieses Beispiel zeigt, dass eine Korrektur von Kontaktwinkeldaten, welche Wenzels Annahmen als einzige Grundlage nutzt, nicht zu empfehlen ist. Durch Messung sowohl der Rauheit als auch des Kontaktwinkels lässt sich jedoch in der Praxis oftmals eine empirische Lösung finden, um die Effekte von Rauheit und Oberflächenenergie auf das Benetzungsverhalten getrennt untersuchen und schließlich auch vorhersagen zu können.

Hintergrund

Benetzung strukturierter Oberflächen – Cassie-Baxter und Wenzel-Zustände

Neben ihrer chemischen Zusammensetzung hat auch die Topografie einen Einfluss auf das Benetzungsverhalten einer Oberfläche. Hierbei wird zwischen zwei Fällen unterschieden: Dringt die Flüssigkeit eines applizierten Tropfens in die (Mikro-)Strukturen ein und verdrängt die darin befindliche Luft, so spricht man von einem Wenzel-Zustand (Abb. 1, links). [1] Verbleiben Lufteinschlüsse in den Strukturen so spricht man von einem Cassie-Baxter- Zustand (Abb. 1, rechts). [2]

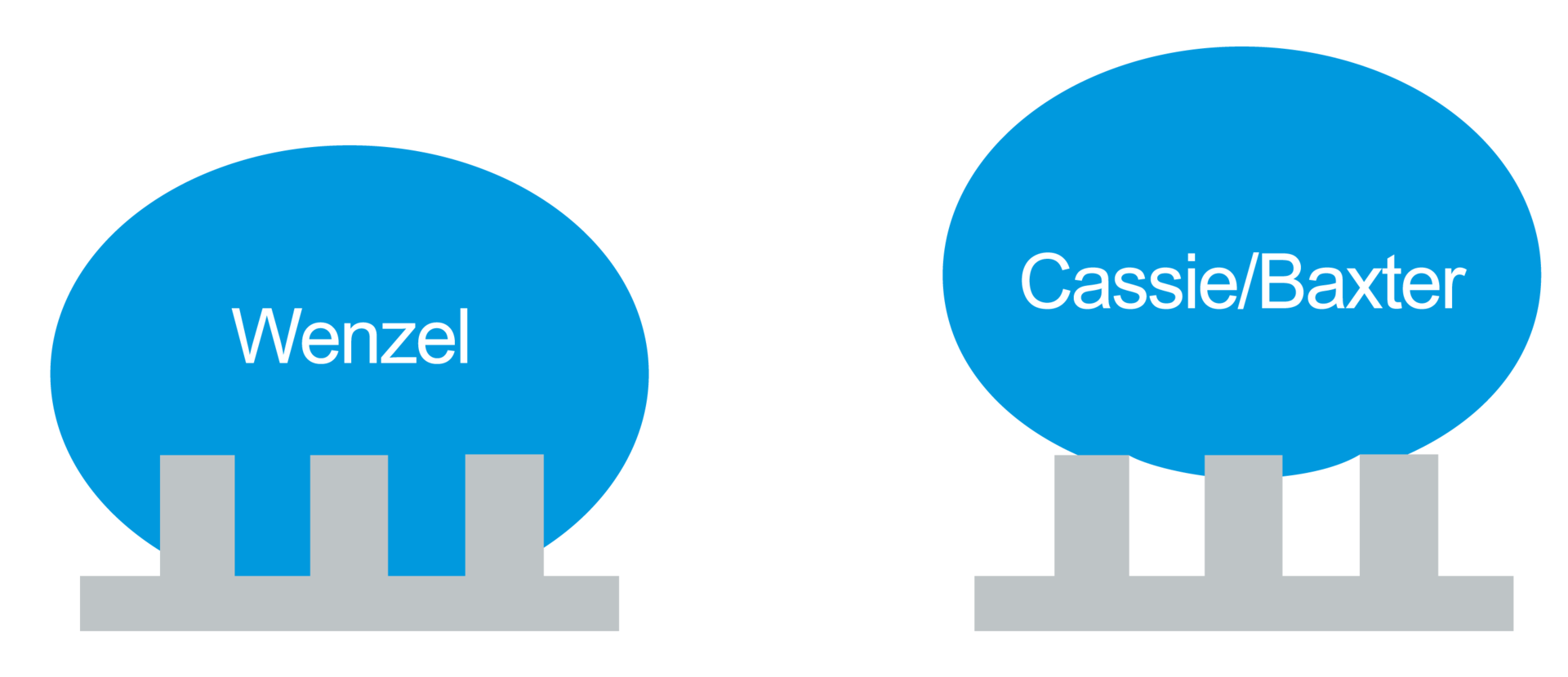
Welcher Zustand vorliegt hängt u.a. von der Größe und Form der Strukturen, der freien Oberflächenenergie des Grundmaterials sowie der Oberflächenspannung der Flüssigkeit ab.

Gemäß Wenzel gilt folgender Zusammenhang zwischen dem Young’schen Kontaktwinkel θ auf einer unstruk­turierten Oberfläche und dem Kontaktwinkel θ* auf einer strukturierten Oberfläche desselben Materials: [1]

Der Rauheitsfaktor r entspricht dem Verhältnis zwischen geometrischer und projizierter Oberfläche der Mikrostrukturen:

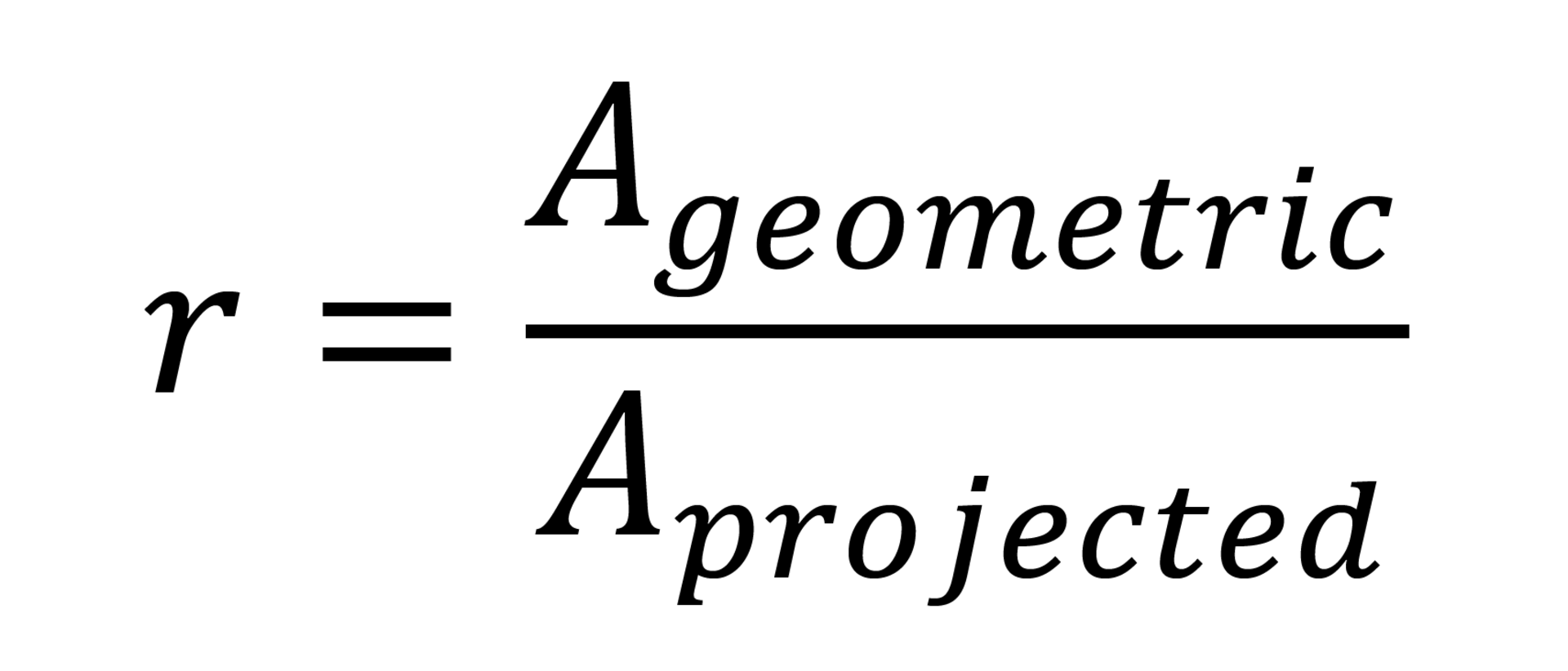
Da die projizierte Oberfläche nicht größer sein kann als die geometrische, ist r immer ≥ 1. Daraus folgt, dass nach der Wenzel-Gleichung der Kontaktwinkel durch die Strukturierung unterhalb von 90° kleiner und oberhalb von 90° größer wird. 90° ist gleichzeitig der Grenzwinkel der Benetzbarkeit, sodass hygrophile Materialien noch hygrophiler und hygrophobe noch hygrophober werden.

Bei Betrachtung dieser Gleichungen ist es scheinbar leicht möglich, bei Kenntnis von θ und r das Benetzungsverhalten strukturierter Oberflächen vorher­zusagen. Umgekehrt ließe sich ermitteln, welchen anteiligen Effekt technische Prozesse wie Sandstrahlen oder Plasmaaktivierung jeweils auf Oberflächenrauheit (r) und freie Oberflächenchemie in Form des Kontaktwinkels auf einer ideal glatten Oberfläche (θ) haben. Ob die Wenzel-Gleichung in der Praxis eine solche direkte Korrektur erlaubt, wurde von uns im Rahmen dieses Berichtes untersucht.

Experimenteller Teil

Probenvorbereitung

Als Festkörperproben wurden von der Firma 5microns GmbH (Ilmenau, Deutschland) aus einem Siliziumwafer unterschiedlich strukturierte Chips gesägt. Die Strukturen wurden dabei anisotrop durch reaktives Ionenätzen realisiert. Eine schematische Darstellung der strukturierten Siliziumchips ist in Abb. 2 gezeigt. Es handelt sich dabei um offene Strukturen, welche im Gegensatz zu invers aufgebauten, geschlossenen Strukturen ein Entweichen von Luft bei Benetzung durch Flüssigkeit erlauben. Die Grabenbreite A wurde dabei zwischen 5 und 50 µm variiert, die Strukturgröße B zwischen 10 und 50 µm. Zieltiefe der Strukturen waren jeweils 5 µm. Unabhängig von der Zielstruktur wiesen alle Proben dieselbe, einheitliche chemische Struktur der Oberfläche (Siliziumdioxid) auf.

Der Rauheitsfaktor r berechnet sich bei den hier verwendeten Strukturen gemäß:

Analyse der Oberflächenstruktur

Die Oberflächenstruktur der Siliziumchips wurde jeweils mit einem Twip Consigno Konfokalmikroskop gemessen. Die Verwendung einer Mikrolinsentechnik ermöglicht bei diesem Instrument hohe Lichtausbeuten, wodurch sich selbst sehr dunkle oder gar transparente Proben mit hoher axialer Auflösung vermessen lassen. Andere gängige Verfahren, wie Triangulation/ Streifenlichtprojektion, sind in ihrer Anwendung eingeschränkt, z. B. durch Limitierung des Höhen­messbereichs bei gleichzeitig geringer Auflösung, durch Probleme bei unterschiedlich reflektierenden Proben sowie aufgrund von „Shadowing“-Effekten, durch welche Strukturen verdeckt und somit übersehen werden können. Die Messungen wurden mit einem Objektiv mit 100-facher Vergrößerung durchgeführt. Die gescannte Fläche betrug jeweils 0,19 × 0,15 mm² bei einem Höhenbereich von 15 µm. Für die Messungen wurde die Software „itom“ verwendet. Zur Bestimmung von r wurde auf die aufgenommenen Bilder ein 0,8 µm Roughness-Cutoff-Filter angewendet.

Kontaktwinkelmessungen

Kontaktwinkelmessungen wurden mit einem KRÜSS Drop Shape Analyzer – DSA100 durchgeführt, unter Verwendung der Software ADVANCE. Hierzu wurden je Chip fünf Tropfen doppelt destillierten Wassers mit Hilfe einer softwaregesteuerten Nadeldosierung abgesetzt und deren Gleichgewichtskontaktwinkel (KW) bestimmt. Das Tropfenvolumen betrug 2 µL, alle Messungen wurden bei 23 ± 0,5 °C durchgeführt. Als Ergebnis ist jeweils der Mittelwert mit Standardabweichung für alle KW-Werte je Probe angegeben.

Ergebnisse

Berechnete und gemessene Rauheitsfaktoren r

Abbildung 3 zeigt die Oberflächentopografie einer exemplarischen, mikrostrukturierten Probe. Die Abmessungen der Strukturen stimmen gut mit den vom Hersteller 5microns GmbH angegebenen Maßen überein.

Anhand der gemessenen topografischen Dimensionen der Proben ermittelt die Software den in der Wenzel-Gleichung verwendeten Rauheitsfaktor r. In Abbildung 4 sind die experimentell ermittelten sowie die gemäß der Zielgeometrie der Strukturen berechneten Werte für r für alle untersuchten Proben aufgetragen. Gemessene und theoretische Werte stimmen gut überein, die größte Abweichung liegt bei unter 5 % (Probe 5‑10).

Kontaktwinkel

Um zu untersuchen, ob das Benetzungsverhalten der strukturierten Proben der Vorhersage von Wenzel folgt, wurden Kontaktwinkelmessungen mit Wasser als Testflüssigkeit durchgeführt (Abb. 5). Bei Strukturen mit niedrigen r-Werten ist die Mikrostruktur teilweise in den Tropfenbildern sichtbar (vgl. Abb. 5, unten).

Abweichung vom postulierten Verlauf gemäß Wenzel

Die Ergebnisse der Kontaktwinkelmessungen sind den entsprechenden r-Werten der Proben in Abbildung 6 gegenübergestellt. Dort ist außerdem der erwartete Verlauf ausgehend von der Wenzel-Gleichung gezeigt, basierend auf einem Kontaktwinkel von θ = 35,18°, der auf dem unstrukturierten Siliziumchip gemessen wurde. Es ist deutlich zu erkennen, dass verglichen mit dem anhand von Wenzels Theorie vorhergesagten Verlauf ein gegenläufiger Trend der resultierenden Kontaktwinkel in Abhängigkeit zu r beobachtet wird. Eine hydrophile Oberfläche wird hier durch Oberflächenstrukturierung hydrophober und nicht hydrophiler.

Diese Diskrepanz zwischen Vorhersage und Messwerten kann vielerlei Ursachen haben, welche im Detail zu diskutieren den Rahmen und auch den Anspruch dieses Berichts sprengen würde. In der wissenschaftlichen Literatur findet sich eine Vielzahl von Veröffentlichungen, welche sich umfassend mit den Bedingungen für Wenzel- und Cassie-Baxter-Zustände sowie deren Übergänge ineinander beschäftigen. Bei Interesse sei exemplarisch auf die Arbeiten von Park et al. verwiesen. [3] Das klare Ergebnis unserer Untersuchungen lautet, dass selbst bei sehr wohldefinierten Oberflächenstrukturen und Wasser als gängigster Testflüssigkeit eine einfache Vorhersage des Benetzungsverhaltens durch die Wenzel-Gleichung nicht ohne weiteres möglich ist. Zwar gibt es Beispiele, in denen die Wenzel-Beziehung eine Vorhersage erlaubt. In der Praxis führt jedoch um Kontaktwinkelmessungen und Messungen der Oberflächenstruktur mit einem geeigneten Verfahren wie der Konfokalmikroskopie kein Weg herum, wenn es um verlässliche Ergebnisse geht.

Entwicklung eines empirischen Modells als praktikable Alternative

Praktisch relevant ist hingegen die Möglichkeit, basierend auf den hier gezeigten Messergebnissen einen eigenen empirischen Zusammenhang zwischen r-Parameter und Kontaktwinkel zu ermitteln. Dieser lässt sich in unserem Beispiel nutzen, um den Einfluss unterschiedlicher Strukturierungen der Oberfläche auf das Benetzungsverhalten vorherzusagen, oder auch den Kontaktwinkel auf einer komplett unstrukturierten Oberfläche (r = 1) extrapolieren zu können (vgl. Abb. 6, hellblaue lineare Anpassung). Dies wiederum zeigt, welchen Einfluss eine Vorbehandlung nur auf die Oberflächenchemie unabhängig von Rauheitseffekten hat.

Zusammenfassung

Wenzel beschreibt in einer einfachen Gleichung, wie die Oberflächenrauheit r die Benetzung einer Oberfläche in Form des Kontaktwinkels beeinflusst. Hier wurde diese Gleichung einem Praxistest unterzogen, indem Wasser-Kontaktwinkel auf wohldefinierten Oberflächen gleicher chemischer Zusammensetzung aber unterschiedlicher Oberflächenrauheit zwischen r = 1 und r = 1,89 gemessen wurden. Dabei wurde gezeigt, dass sich die Oberflächentopografie mikrostrukturierter Proben konfokalmikroskopisch sehr präzise ermitteln lässt.

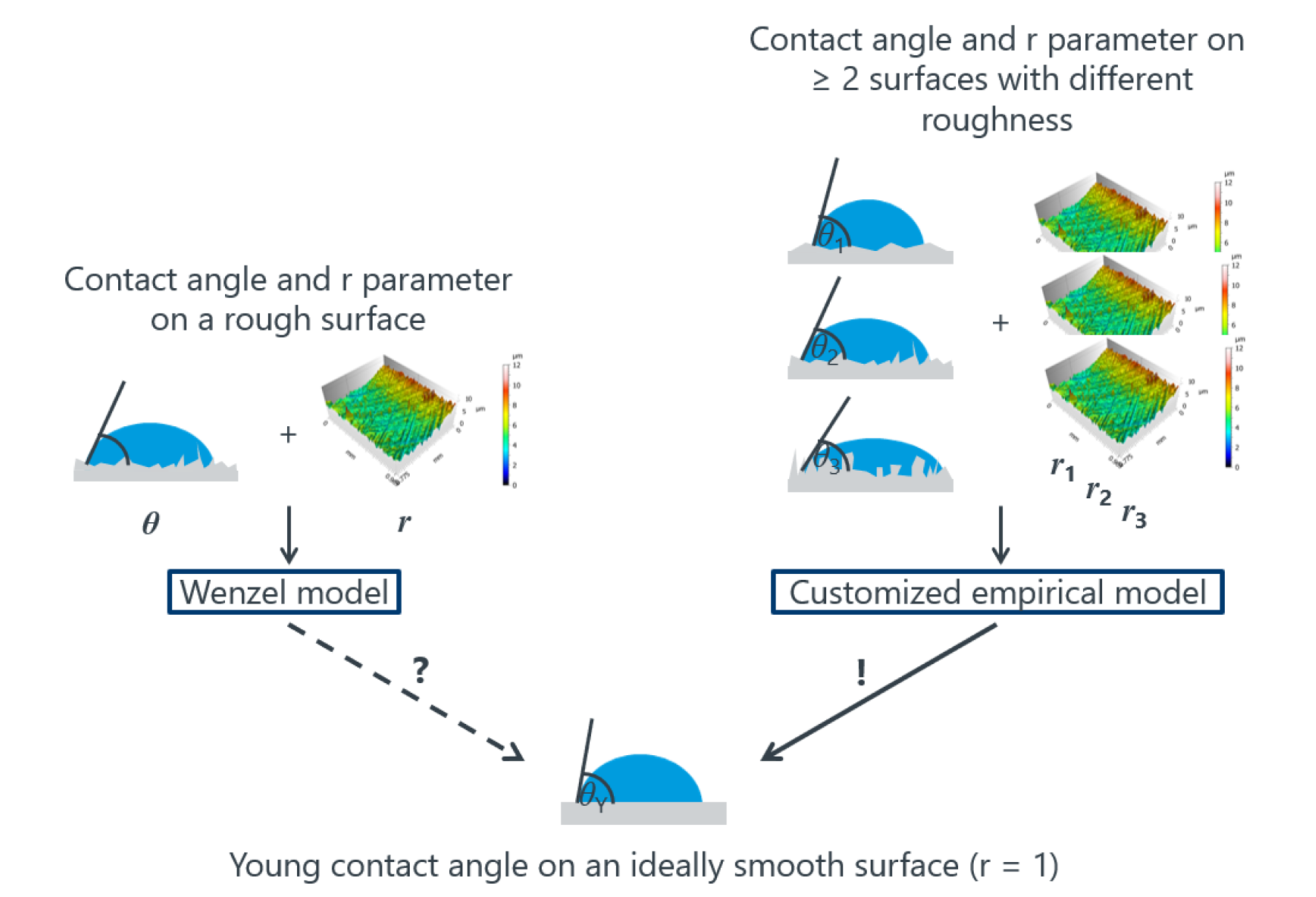
Entgegen der Vorhersage gemäß der Wenzel-Gleichung wurde experimentell ein umgekehrter Trend für den Verlauf des Kontaktwinkels bei steigender Rauheit beobachtet. Benetzung wird sowohl von dem Material der Oberfläche als auch deren Topografie bestimmt. Ist der Kontaktwinkel auf einer strukturierten Oberfläche bekannt, darf nicht blind darauf vertraut werden, mit der Wenzel Gleichung auch den Young-KW auf einer glatten Oberfläche gleichen Materials vorhersagen zu können. Anhand der beschriebenen Messungen kann die Gültigkeit der Wenzel-Gleichung in der Praxis überprüft und gegebenenfalls durch einen einfachen empirischen Zusammenhang ersetzt werden (Abb. 7). Dieser wiederum erlaubt dann eine Extrapolation des Benetzungsverhaltens für unstrukturierte Oberflächen und eine Abschätzung, in welchem Maße jeweils Oberflächenchemie und Oberflächenrauheit das Benetzungsverhalten beeinflussen.

Literatur

• [1]   R. N. Wenzel, “Resistance of Solid Surfaces to Wetting by Water”, Ind. Eng. Chem. 28, Nr. 8, S. 988–994, (1936).

• [2]   A. B. D. Cassie, S. Baxter, “Wettability of Porous Surfaces”, Trans. Faraday Soc. 40, S. 546–551, (1944).

• [3]   C. I. Park, H. E. Jeong, S. H. Lee, H. S. Cho, K. Y. Suh, “Wetting transition and optimal design for microstructured surfaces with hydrophobic and hydrophilic materials”, J Colloid Interf Sc 336, S. 298–303, (2009).